�@���w�U�i��j���|�[�g�쐬�q���g�W
��V�ۑ�
�� ��ʊp
���ȏ��o�U�U�D�o�U�V���悭�ǂ�ł����ł���Ƃ������܂��B
�Q�D�͂R�O���̓��a�̈ʒu�ł̈�ʊp�̕\���̎d���ł��B
�@�@���O�p��
�@�@�@�@���ȏ��o�U�W�̒�`�𐳊m�ɂ���ł��������B
�@�@�@�@�R�D�́i�P�j�͂o�U�X�̖�R�́i�P�j�A�i�Q�j�́i�Q�j�̍�}�̎d���ƍl���͓����ł��B
�@�@���O�p���̑��݊W
�@�@�@�@�S�D�͂o�U�W�̒�`�ł����P�Ƃ������́B
�@�@���O�p���̃O���t
�@�@�@�@�P�D�Q�D�̃O���t�͋��ȏ��o�V�Q�̃O���t�ɂȂ�܂��B
�@�@�@�@�R�D�i�P�j�����͂���sin�Ƃ̎����Ɠ����ł����i�Q�j�i�R�j�̏ꍇ�͂��ꂼ��R�Ɓ��R�U�O���A�Q�Ɓ��R�U�O������o���܂�
�@�@�@�@�@�@�i�R�j�̃O���t�͋��ȏ��o�V�S��X�D�Q��
�@�@�@�@�@�@y=tan�Ƃ̃O���t�͋��ȏ��o�V�T�Q��
��W�ۑ�
�� �O�p���̐���
�P�D�i�Q�j�i�S�j��cos�i-�Ɓj��cos�Ƃ��g���Ă���A�i�P�j�i�R�j�i�S�j�͂O������X�O���͈̔͂̊p�x�ɂȂ����Ăo�P�S�T�̕\���g���܂��B
�@�@�����@�藝
�@�@�@�@�R�D�S�D���Q�D�R�ƂȂ�܂����A�o�W�P�`���W�Q�𐳊m�ɂ��̂܂ܓ��ւ���Ă��������B
�@�@�@�@�T�D���S�D�ƂȂ�܂����A���ȏ��o�W�P�̗�Q�D��R�̍l���������̂܂܂ł��B
�@�@���ʓx�@
�@�@�@�@�U�D���T�D�ƂȂ�܂����A�@��{�́@�P�W�O�������W�A���@�Ɗo���Ă��������B���ꂩ��o���オ�����\�����W�S�̉��ɂ���܂��B
�@�@�@�@�V�D���U�D�ƂȂ�܂��B����͂��W�T�̗�U�D�Q�Ƃłn�j�D�ł�
�@�@�a�̂P�D�i�P�j���ȏ��o�W�R�̏�i���悭�ǂ߂ΐ����ɂȂ���܂�
�@�@�@�@�@�@�i�Q�j�͌������̂���
�@�@�@�@�Q�D�o�W�R�̗�S�D�Ɩ�S�D�ɂ����肻�ꂼ�ꃿ���S�T���A�R�O���̏ꍇ�ɂȂ�܂��B
�@�@�@�@�@�����ŋ��ʂ��đ�Ȃ��Ƃ́A���p�O�p�`�̂S�T���S�T���X�O���ƂR�O���U�O���X�O���̕ӂ̔�ɂ���Ă������Ƃ��A��ł��B
�@�@�b�́A���A���͉s�p�Ȃ̂ŁA�O�p�`������Ă��ꂼ��i�P�j�i�Q�j���o���܂��B�i�R�j�i�S�j�͂o�W�P�̌������p�ł��B�i�T�j��
�@�@�@�@tan�Ɓ�sin��/cos�Ƃ̍l���������X�O�ł��B
��X�ۑ�
�@�@�@�P�D�`�R�D�́A���ȏ����W�W�`�o�W�X�Q�Ƃł����A�Ƃ��ɂR�D�i�R�j�͂O�D�O�P���P/�P�O�Q���P�O�|�Q�ƃJ�b�R�̂Ȃ����Ă���v�Z�ł�
�@�@�@�@�T�D�U�D�V���S�D�T�D�U�ƂȂ�܂����A���ȏ����X�R�̗��P�D�𒆐S�̊w�K���Ă��������B
�@�@�@�@�W�D���V�D�ƂȂ�܂��B���X�S�`�X�T�̗�P�O��P�P�ɂȂ�܂��B
�@�@�@�@�X�D���W�D�ƂȂ�܂����A����͋��ȏ��o�X�U���Q�D�ƂȂ�܂��B
�@�@�@�P�O�D���X�D�ƂȂ�܂����A�o�X�U��P�Q�A��P�T�Q�Ƃ��Ă��������B
�@�@�@�P�P�D�P�Q���P�O�D�P�P�ƂȂ�܂����A���ȏ��o�X�W�`�X�X�̏����������K�ɂȂ�܂��B���ɂo�X�W�̍ʼn��i�̐}�ɂ���Ă������Ƃ�
�@�@�@�K�{�ł��B
�@�@�@�P�R�D���P�Q�D�ƂȂ�܂����A���ȏ��o�P�O�O�D��R�D�̍l���ɂȂ�܂��B
�@�@�@�P�S�D���P�R�D�ƂȂ�܂����A���ȏ��o�P�O�P�̗��Q�A��V�Q��
�@�@�@�P�T�D���P�S�D�ƂȂ�܂����A�i�P�j�R�D�S�W�͂o�P�S�U���̂܂ܗ��p�B�@�i�Q�j�͂P�R�S�O���P�D�R�S�~�P�O�R�ƕό`���Ă���o���܂��B
�@�@�@�P�U�D���P�T�D�ƂȂ�܂����A���ȏ��o�P�O�P�̗��R�D��W���Q�Ƃ��āA���Ă��������B
��10�ۑ�ɂ͂���܂����i�����ւ̂����߁j
���P�����Ƃ͉���
��@�����N��A�n�_���ߌ�P���ɏo�����AB�n�_�Ɍߌ�U���ɒ������BA�n�_����B�n�_�܂�20��������B
�����͂ǂꂾ���H
�@�@�@�@�����@20���T���S�@���@�P�ʂ�t���ā@�Skm/���@�ƂȂ�
�u����������ŗǂ����낤���H�v
�@�@�@�����Ȃ�����A�x���Ȃ�����A��x�݂��邱�Ƃ�����ł��傤�B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���͂���́A���ϑ��x�Ƃ����܂��B
�V�C�\��Ȃǂł́A�u�ԕ����������[�g���Ƃ����̂��L��ł��傤�B
����͏u�ԑ��x�Ƃ����̂\���Ă���̂ł��B
�@�|�u�ԑ��x�̋��ߕ��|
�@��̖��ŁAC�n�_���R���ɒʉ߂��Ă���B�b�n�_�ł̈����N�̏u�ԑ��x�͂ǂꂾ�����낤�B
A�n�_����C�n�_�܂ł̋�����9�����ł������Ƃ���B
��
�̓f���^�Ɠǂ� ���� �� �f���^�G�b�N�X�ł�
3��1���̂Ƃ��͂`�n�_����̋�����9.7����
3��30�b�̂Ƃ��͂`�n�_����̋�����9.4����
3���P0�b�̂Ƃ��͂`�n�_����̋�����9.1����
3���P�b�̂Ƃ��͂`�n�_����̋�����9.01����
3��0.�P�b�̂Ƃ��͂`�n�_����̋�����9.001����
![]()
![]() �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���̂悤�ɂǂ�ǂԂ�3���ɋ߂Â��܂�
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���̂悤�ɂǂ�ǂԂ�3���ɋ߂Â��܂�
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�R�������i���͂������O�ɋ߂����j�̂Ƃ��@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
3�� h�b �@�@�@�@�@�@�@ �i�X�{�����j���� �@�`�n�_����̋������i�X�{�����j�����Ƃ��܂��B
����3������3�������܂ł̕��ϑ��x�́@![]() �@�@�ŋ��߂��܂�
�@�@�ŋ��߂��܂�
�@�@�@�����Ă��̂�������������������Əu�ԑ��x�ƂȂ�܂��B�@
�܂��A���̌���Ȃ��O�ɋ߂Â���Ƃ����L���� ![]() �ł��B�@�@�܂�@
�ł��B�@�@�܂�@![]() km/��
km/��
�@�@�@���ꂪ�u�ԑ��x�ł��B
�����I�ɂ́@0.0000001�b���炢�ɉ����i���Ōv�Z���܂��@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
���ϑ��x���u�ԑ��x���@�P�ʁukm/���v������܂��ˁB��₱�����̂ŒP�ʂ���菜����
���ϑ��x�́u���ϕω����v�@�u�ԑ��x�́u�����W���v�ɂȂ�܂��B
�u�ԑ��x��3���̂Ƃ��A�Ƃ����̂������̂Ƃ��Ƃ��܂��B�܂肘���ɂ�����u�ԑ��x�B���ꂩ��P�ʂ����������̂��u�����v�Ƃ����܂��B���̓��������߂邱�Ƃ��A�u��������v�Ƃ����̂ł��B
��10�ۑ�
�P.
![]()
![]() ����͐��l�����邾�����������ł��傤�B���������l������Ƃ��Ɂi�j��Y��Ȃ��łˁB
����͐��l�����邾�����������ł��傤�B���������l������Ƃ��Ɂi�j��Y��Ȃ��łˁB
��@![]()
![]() �Ł@
�Ł@![]() �@�̒l�����߂�ƁA
�@�̒l�����߂�ƁA
�@�@�@�@�@�@�@�@�@�@�@�@�@�@![]() �@
�@
�@�Q.�@����͕��ϑ��x�����߂���ł��B
�@�P�b��@�Ɓ@3�b��@���������߂ā@�����������ԁi���̏ꍇ�́@3�|�P�@�b�j�Ŋ���
�@���ӁE�E�E�P�ʂ�Y��Ȃ��悤�Ɂ@��/�b
�@�R.�@���ϕω��������߂���ł��B�P�ʂ͗v��܂���@
��@![]() �@�ɂ����ā@
�@�ɂ����ā@![]() ���|�Q����R�܂ŕω�����Ƃ��̕��ϕω��������߂��
���|�Q����R�܂ŕω�����Ƃ��̕��ϕω��������߂��
�@�@�@![]() �@�@�@�@
�@�@�@�@![]()
�@�@�@����ā@![]() �@�@�@�@�܂肱�̏ꍇ�̕��ϕω����́@�S�@�ł��@
�@�@�@�@�܂肱�̏ꍇ�̕��ϕω����́@�S�@�ł��@
�S. ����͂���0�ɂ��邾���ł��B�@��ԊȒP
��@![]() �@�̏ꍇ�����O�ɂ��ā@�@
�@�̏ꍇ�����O�ɂ��ā@�@![]() �@�ł�
�@�ł�
�T. �����ł̔����ł��B�ЂƂ��������܂��E�E�E����������̂ɂ́e�@�����܂��B
��@![]()
�@�@�@�@�@�@�@�@�@��������Ɓ@�@![]() �@�ƂȂ�܂�
�@�ƂȂ�܂�
![]() �������Ŕ�������Ɓ@
�������Ŕ�������Ɓ@![]() �ɂ������Ă���w���R��O�ɏo���Ă�����B�w����1�����@
�ɂ������Ă���w���R��O�ɏo���Ă�����B�w����1�����@
������@![]() ���������ƁA
���������ƁA![]() ��
��![]() �@�ƂȂ�܂��B�@
�@�ƂȂ�܂��B�@
���l�ɂ��ā@![]() ���������ƁA
���������ƁA![]() �@�ƂȂ�܂��B�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�@�ƂȂ�܂��B�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�@�@�@
![]() �̏ꍇ�͎w���͂P�ł��B�@�w������P�������ƂO�ƂȂ�܂��ˁB
�̏ꍇ�͎w���͂P�ł��B�@�w������P�������ƂO�ƂȂ�܂��ˁB
�O��͂����P�ł��B�܂���������1�~�Q�~�P�� �Q�ƂȂ�܂��B�@
�܂�w�����P�̎��͑O�̐������ɂȂ�̂ł��B
�|�T�̏ꍇ�́@�����݂̂ł��ˁB���̂悤�ɐ����݂̂̍��́A�萔���Ƃ�����
�O�ƂȂ�܂��B�u�����݂̂̒萔���͔�������ƂO�v
�@�@�@������S�����ׂď����Ώo���オ��B
�S.
�T.�Ɠ����ł��B�@����肪![]() �@�ƂȂ��Ă���̂ŁA�����̎n�܂肪
�@�ƂȂ��Ă���̂ŁA�����̎n�܂肪 ![]() �ł͂Ȃ��A
�ł͂Ȃ��A![]() ��
��
�@�V. (1),(2)�͏ȗ��@(3)�́@(2)�Ŕ����������̂Ɂ@![]() �@��������B�J�b�R��Y��Ȃ�����
�@��������B�J�b�R��Y��Ȃ�����
�@�W.�@�u���������߂�v�Ɓu��������v�Ƃ����̂͂܂����������Ӗ��ł��B�@�@�X. �͏ȗ�
�P�O. �������āA![]() �@��������B�@�P�ʂ�Y��Ȃ����Ɓ@���̏ꍇ�̒P�ʂ́u��/�b�v
�@��������B�@�P�ʂ�Y��Ȃ����Ɓ@���̏ꍇ�̒P�ʂ́u��/�b�v
![]() �P�P. �Q�l��@�@�u�Ȑ��@
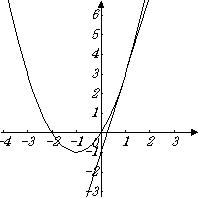
�P�P. �Q�l��@�@�u�Ȑ��@![]() �@�@��̓_�i�|�P,�R�j�ɂ�����ڐ��̌X�������߂�v
�@�@��̓_�i�|�P,�R�j�ɂ�����ڐ��̌X�������߂�v
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���̒l������
![]()
![]() �@
�@![]() �@���X���́@
�@���X���́@![]() �@�@�@
�@�@�@
![]() �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���̒l(�|�U)���A�ڐ��̌X���ł�
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���̒l(�|�U)���A�ڐ��̌X���ł�
�@�@�@�@�@�@�q���g�@(1) �������āA�Q������@�@�@(2) �������āA�|�R������
�P�Q. �ڐ��̋��ߕ��@���̓�̌�����g�ݍ��킹��B
�@�����P�@�_![]() ��ʂ�A�X���� �̒����̎���
��ʂ�A�X���� �̒����̎��� ![]() �@
�@
�����Q�@�ړ_��![]() �ł���A�ڐ��̌X������
�ł���A�ڐ��̌X������![]() �@
�@
![]() �@�@�@�Q�l��@�@�u�Ȑ��@
�@�@�@�Q�l��@�@�u�Ȑ��@![]() �@��̓_�i�P�C�R�j�ɂ�����ڐ��̕����������߂Ȃ����v�@�@�@
�@��̓_�i�P�C�R�j�ɂ�����ڐ��̕����������߂Ȃ����v�@�@�@

 �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���̒l������
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���̒l������
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@![]() ���@
���@
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�ڐ��̌X���́@�Q(�P�j�{�Q���Q�{�Q���S�@�������Q��聄
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�ڐ��́@![]() �@�������P��聄
�@�������P��聄
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@![]() �@
�@

![]() �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@![]() �@�@�@�@�����@
�@�@�@�@�����@![]()
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���P�Q. �́@
![]() �@��������ā@�ڐ��̌X�������߂�@
�@��������ā@�ڐ��̌X�������߂�@
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���Ɂ@�����P���ڐ������߂�@�@�@�@�@�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���P�R.�� �P�Q�Ɠ����Ȃ̂ŏȗ�
�P�S. �@�P�Q�̌����@�u�ڐ��̌X������![]() �v������g��
�v������g��
�@�@(1) ![]() �@���@�X���́@
�@���@�X���́@![]() �@�@�����X���͂Q������@�@
�@�@�����X���͂Q������@�@
�@�@ ![]() �@�v�Z���ā@
�@�v�Z���ā@![]() �@���ꂪ�ړ_��
�@���ꂪ�ړ_��![]() ���W�ƂȂ�B
���W�ƂȂ�B
�@�@ �ړ_��![]() ���W�́@
���W�́@![]() �@�Ɂ@���̂R�������ā@
�@�Ɂ@���̂R�������ā@![]() �@�ŋ��߂�B
�@�ŋ��߂�B
�@�@�@�@
�ړ_�̍��W�́i�ړ_��![]() ���W�C�ړ_��
���W�C�ړ_��![]() ���W�j�@�ł���
���W�j�@�ł���
(2) (1)�ŋ��߂��A�ړ_��ʂ�ڐ��̎������߂�B�X���͂Q�ł���B
�P�T. ��`�ɏ]���Ĕ����W���⓱���i�����j�����߂���@
�@�Q�l��@�u���@![]() �@�ɂ����ā@
�@�ɂ����ā@![]() �@�̔����W�����`�Ɋ�Â��ċ��߂Ȃ����v
�@�̔����W�����`�Ɋ�Â��ċ��߂Ȃ����v
�@�@�@![]() �@�@�@�@�@
�@�@�@�@�@![]() �@�@
�@�@
�@�@�@![]()
![]()
![]()
![]()
�Q�l��@�u���@![]() �@�����`�Ɋ�Â��Ĕ������Ȃ����v
�@�����`�Ɋ�Â��Ĕ������Ȃ����v![]()
![]()
![]()
![]()
![]()
![]()
![]()
�����P�T�̉��������@�����W���̖��ł́A�ŏ���![]() ��
��![]() �@�����߂Ă���
�@�����߂Ă���
�@�@�@�@�@�@�@�@�@�@�@�����̖��ł́A�ŏ���![]() ��
��![]() �@�����߂Ă���
�@�����߂Ă���
�@�@�@�@�@�@�@�@�@�@�@�v�Z�̓r���ł�������Ԃ͏�Ɂ@![]() �@�����[�Ə�������
�@�����[�Ə�������
�@��P�P�ۑ�
�� �����E����![]()
�P�D��ɁA�s�����Q�ix�\�Q�j![]() �O�A�Q�i���|�Q�j
�O�A�Q�i���|�Q�j![]() �O���Ƃ��āAx�͈̔͂��o���܂��B���ȏ��o�P�P�W�`�P�P�X�̗�P�D��Q�A���P�Q��
�O���Ƃ��āAx�͈̔͂��o���܂��B���ȏ��o�P�P�W�`�P�P�X�̗�P�D��Q�A���P�Q��
�� �ɑ�E�ɏ�
�Q�D�s����3x�ix�\�Q�j![]() �O�C�Rx�ix�\�Q�j
�O�C�Rx�ix�\�Q�j![]() �O���Ƃ��āA�ɑ�ƂȂ�͈́A�ɏ��ƂȂ�͈͂��o���܂��B���ȏ��o�P�Q�P�̗�R�A���Q
�O���Ƃ��āA�ɑ�ƂȂ�͈́A�ɏ��ƂȂ�͈͂��o���܂��B���ȏ��o�P�Q�P�̗�R�A���Q
�@�̍l���Ɠ��l�ɂł��܂��B
�R�D�o�P�Q�P�̗�R�A���Q�����ȏ��������ɂł���悤�ɂȂ�A�i�P�j�`�i�U�j�͒��J�ȗU���`���ɂȂ��Ă���̂ŁA�Ȃ�Ȃ��ł���������
�����ł��傤�B
�@�@�@�a�P�D�Q�D�͏�̂R�D���Ƃ�肩���́A�����ł��B
�P�D�͂o�P�Q�P�̗�R�̃O���t�̃^�C�v�A�Q�D�͂o�P�Q�P�̗��Q�̃O���t�̃^�C�v�ƂȂ�܂��B
�@�b�D�����J�ɗU���`���ɂȂ��Ă��܂��B���ȏ��o�P�Q�Q�̗��R�D�ƑΔ䂵�Ȃ���i�߂Ă����A�e�Ղɂł��܂��B
�@��P�Q�ۑ�
���s��ϕ�
�@�@�P�D�i�P�j�A�i�Q�j�͋��ȏ��o�P�Q�S�ɏ�����Ă�����e������₢�ɂȂ��Ă܂��B�܂��������A�������������Ă��������B
�@�@�@�@�i�R�j�A�i�S�j�͋��ȏ����P�Q�T�̗�P�D�̓��e�ł��B
�@�@�Q�D�R�D�͋��ȏ��o�P�Q�T�`�P�Q�U�̗��K�ŗ�R�D�̗����ɂƂ߂Ă��������B
����ϕ��̌v�Z
�@�@�S�D�i�P�j�͋��ȏ��o�P�Q�W�̗�S�A�̏�i�ɏ����Ă�����e�������肵�����̂ŁA�܂������𐳂����������Ă��������B
�@�@�T�D�͋��ȏ��o�P�Q�W�`�P�Q�X�̗�S�A��T�A��U�̓��e�ɂȂ�܂��B
�@�@�@�@�i�S�j�ł͂��Ƃ��Δ�ϕ����i�C���e�O�����L���̂Ȃ��ɂ���j���ix�{�P�j�Q�̂Ƃ��W�J���Ă���Ƃ肩�����ɂȂ��Ă܂��B
�@�@�a
���ʐ�
�@�@�i�P�j���ȏ����P�R�O�̒�����y��x��y��x�{�P�ɂ�������`�ł��B
�@�@�i�Q�j���ȏ����P�R�P�̗�V�i�R�j�͋��ȏ��o�P�R�P�̗�W�D�i�S�j�͋��ȏ����P�R�Q�̗��R�ɑΉ����Ă܂��B���������x�����肩����
�@�@�@�@�@����ė����ɂƂ߂Ă��������B
�@�@�b�A�̖��͂o�P�R�S�̗��S�D�Q�Ƃł����@
�@�@�i�P�j�́[x�{�P��x�Q�{�Sx�|�T����A�������ĂQ�����������Ƃ��āAx�������܂��B
�@�@�i�Q�j�`�i�S�j�͖��̎w���ɂ��������Ă����߂Ă��������B
�@�@
![]()