丂
悢妛嘥乮慜乯儗億乕僩嶌惉僸儞僩廤
丂
丂戞侾曬崘壽戣乮彫悢丒暘悢丒惓晧偺悢乯
丂丂仢彫悢
丂丂丂丂侾丏乮侾乯丄乮俀乯偱偼丄彫悢揰偺埵抲傪偦傠偊偰寁嶼偟傑偡丅
丂丂丂丂丂丂乮俁乯偼丄彫悢偑側偄偲偟偰寁嶼偟偰丄寢壥偺悢偵侾侽侽偺埵偲侾侽侽侽偺埵偺娫偵彫悢傪偆偪傑偡丅
丂丂丂丂丂丂乮係乯俁丏侾傪俁侾丄俈侾俁傪俈侾俁侽偲偟偰俈俀俁侾亐俁侾傪寁嶼偡傟偽俷俲偱偡丅
丂丂仢暘悢
丂丂丂丂俀丏暘悢偺惈幙偲偟偰丄乽暘曣暘巕偵摨偠悢傪偐偗偨傝丄摨偠悢偱妱偭偨傝偟偰傕傛偄乿偺惈幙傪偮偐偄傑偡丅
丂丂丂丂俁丏暘悢偺寁嶼
丂丂丂丂丂丂丂丂亊丒丒丒暘曣偳偆偟丄暘巕偳偆偟傪偐偗偁傢偣傞丅
丂丂丂丂丂丂丂丂亐丒丒丒偐偗傞曽偺暘悢偺丄暘曣暘巕傪偄傟偐偊偨暘悢傪偮偔傝偦傟傜偺暘悢摨巑傪偐偗偁傢偣傞丅
丂丂丂丂丂丂丂丂亄,亅丒丒丒暘巕偺悢偺傒偺寁嶼偵側傝傑偡丅
丂丂丂丂係丏巜帵偺偲偆傝偡傟偽俷俲
丂丂丂丂俆丏俇丏偲傕偵暘曣傪捠暘偟偰摨偠偵偟偰偐傜寁嶼偟傑偡丅
丂丂仢惓偺悢丒晧偺悢
丂丂丂丂俈丏
亄乮亄乯仺亄丄亄乮亅乯仺乕丄亅乮亄乯仺乕丄亅乮亅乯仺亄偱乮丂乯傪偼偢偟偨偁偲丄摨晞崋偺偡応崌偼丄晞崋傪偲偭偨悢傪偨偟偰寢壥偵偦偺晞崋
丂丂丂丂丂丂丂傪偮偗偰偍偔丅
丂丂丂丂丂丂丂堎晞崋偺偲偒偼丄戝偒偄悢偐傜彫偝偄悢傪堷偄偰寢壥偼戝偒偄悢偺傎偆偺晞崌傪偮偗偰偍偔丅
丂丂丂丂俉丏摨晞崋偳偆偟偺偲偒偼摎偊偺晞崋偼亄丄堎晞崋偳偆偟偺偲偒偼乕偲側傝傑偡丅
丂丂丂丂丂丂丂亅乮亅俀乯俆偵偮偄偰丄亅乮亅傪亄偵曄偊偰偼僟儊両
丂丂丂丂俋丏朄懃偲偼
丂丂丂丂丂丂亊丄亐丄亄丄乕偑擖傝崿偠偭偰偄傞偲偒偼丂
丂丂丂丂丂丂亊丄亐傪愭偵傗傝丄亄丄乕偼偦偺偁偲偵側傝傑偡丅
丂丂仢暥帤偺幃
丂丂丂丂侾侽丏椺偺偲偍傝
丂丂丂丂侾侾丏侾侽偺媡偺峫偊偱寁嶼婰崋傪棯偡傞傫偱偡偑丄偦偺偲偒悢偼寁嶼偟偰偍偒傑偡丅
丂丂丂丂丂丂丂俉亊乮亅俀乯偼乕侾俇偲偟偰偍偒傑偡丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂戞侾曬崘壽戣埲忋偱偡丅幙栤偁傟偽偊傫傝傚偆偣偢偵偳偆偧丅
丂戞俀曬崘壽戣乮暥帤幃丒曽掱幃乯
丂丂丂丂侾丏椺偺偲偍傝偱偡丅側傪乮俁乯偺偲偙傠偼乮侾乯偺娫堘偄偱偡丅掶惓偟偰偍偄偰偔偩偝偄丅
丂丂丂丂丂丂丂a=2,b=亅俁丄們亖亅侾偺偲偒丂丂倐俀 乕ac=(亅俁乯俀丂乕俀亊乮亅侾乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂=俋亄俀
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂=侾侾
丂丂丂丂丂 丂丂丂丂丂丂丂丂丂丂丂丂丂丂偲側傝傑偡丅
丂
丂丂丂丂俀丏偨偲偊偽偺寁嶼丂丂(俇倶亄俀乯亐俁偼丄乮俇倶亄俀乯亐俁丂亖俇倶/俁亄俀/俁
丂丂丂丂丂丂丂丂丂丂丂丂丂 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖俀倶亄俀/俁
丂丂丂丂俁丏摨椶崁傪傑偲傔傞偲偼丄摨偠暥帤偵拲栚偟偰
丂丂丂丂丂丂丂仺倶亄俁倷亄俆倸亅俀倶亅俁倷
丂丂丂丂丂丂丂亖乮倶亅俀倶乯亄乮俁倷亅俁倷乯亄俆倸
丂丂丂丂丂丂丂亖乮侾亅俀乯倶亄乮俁亅俁乯倷亄俆倸
丂丂丂丂丂丂丂亖亅倶亄侽倷亄俆倸
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂偲側傝傑偡丅
丂
丂丂丂丂係丏僇僢僐傪偼偢偡
丂丂丂丂丂丂仺乮倶亄俁倷乯亅乮俀倶亄倷乯
丂丂丂丂丂丂亖倶亄俁倷亅俀倶亅倷
丂丂丂丂丂丂亖乮倶亅俀倶乯亄乮俁倷亅倷乯
丂丂丂丂丂丂亖乮侾亅俀乯倶亄乮俁亅侾乯倷
丂丂丂丂丂丂亖亅倶亄俀倷
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂偲側傝傑偡丅
丂丂丂丂俆丏嫵壢彂椺侾係嶲徠
丂丂丂丂俇丄俈丏嫵壢彂椺侾俆嶲徠
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂戞俀曬崘壽戣埲忋偱偡
戞俁曬崘壽戣乮僌儔僼丒惍幃乯
丂丂仢僌儔僼
丂丂丂丂侾丏丂嵗昗偺揰偺偆偪偐偨偼
丂丂丂丂丂丂丂丂乮倃嵗昗丄倄嵗昗乯偲側偭偰傑偡丅
丂丂丂丂俀丏俁丏係丏俆丏偼嫵壢彂俹丏俆俋偱傑偵偁偄偦偆偱偡丅
丂丂丂丂丂丂丂側偐偱傕丄俁丏係偼倃幉丄倄幉偄偢傟偐偵暯峴側捈慄偵側傝傑偡丅
丂丂丂丂丂丂俆偺乮俀乯偼丂俀倄亖丒丒丒偲曄宍偟偨屻丄椉曈傪俀偱妱偭偰孹偒丄倄愗曅傪弌偟傑偡丅
丂丂丂丂丂丂側傪丄孹偒偑亄偺偲偒偼丄捈慄偼塃忋偑傝丄亅偺偲偒偼丄捈慄偼塃壓偑傝偲側傝傑偡丅
丂丂仢扨崁幃丒懡崁幃
丂丂丂丂俇丏暥帤偺傑偊偵側偵傕悢帤偑側偄偲偒
丂丂丂丂丂丂偨偲偊偽丄俁倃倄偱偼側偔丂丄倃倄偺偲偒偼學悢俷偱偼側偔丄侾偱偡丅
丂丂丂丂俈丏崁傋偒偺弴偲偼丄師悢偺崅偄傎偆偐傜掅偄傎偆傊暲傃懼偊傞偙偲偱偡丅
丂丂丂丂俉丏侾侽乮俋偵側傝傑偡乯偼丄嫵壢彂俹侾俉乣侾俋嶲徠偱俷俲偱偡丅
丂丂丂丂侾侾乮侾侽偵側傝傑偡乯丄侾俀乮侾侾偵側傝傑偡乯偼嫵壢彂俹俀侽乣俀侾嶲徠
丂丂丂丂丂丂偲偔偵丄拲堄偡傞偙偲偼
丂丂丂丂丂丂丂乮俁倃俀乯俁偼俁倃俀丂傪
俁夞偐偗傞堄枴側偺偱俀俈倃俇丂偲
側傝傑偡丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂戞俁曬崘壽戣埲忋偱偡
丂戞係曬崘壽戣乮晄摍幃乯
丂丂仢侾師晄摍幃
丂丂丂丂侾丏嫵壢彂俹俁俉偺椺侾丏嶲徠
丂丂丂丂俀丏嫵壢彂俹俁俉偺椺俀丏嶲徠
丂丂丂丂丂丂嬶懱揑偵偼乕俁偐傜俁傑偱偺抣傪戙擖偡傟偽傢偐傝傑偡丅
丂丂仢晄摍幃偺惈幙
丂丂丂丂堦斣戝愗側偙偲偼丄晄摍幃偺椉曈偵晧偺悢傪偐偗
傞丄偁傞偄偼晧偺悢偱傢傞偲偒偼晄摍崋偺岦偒偑偐傢傞偙偲偵拲堄偱
偡丅
丂丂丂丂俁丏乣俈丏偼嫵壢彂倫係侾乣係係嶲徠
丂丂丂丂俉丏乣俋丏偼嫵壢彂俹係係椺俁嶲徠偱俷俲偱偡丅
丂丂丂丂侾侽丏偼嫵壢彂俹係俆椺係丏嶲徠
丂丂丂丂侾侾丏偼嫵壢彂俹俁俋嶲徠
丂丂丂丂侾俀丏偼嫵壢彂倫係俇嶲徠偲儗億乕僩偺椺傪傛偔妛廗偡傟偽俷俲偱偡丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂戞係曬崘壽戣埲忋偱偡
丂戞俆曬崘壽戣乮揥奐丒場悢暘夝乯
丂丂丂儗億乕僩偺揥奐偺椺丄場悢暘夝偺椺傪傛偔妛廗偟偰偲傝偔傔偽丄惓夝偵摓払偟傑偡丅
丂丂丂丂侾丏乣俁丏偼偦傟偧傟斣崋偺偁偲偺乮丂乯撪偺嫵壢彂偺嶲徠儁乕僕傪傒偰偔偩偝偄丅
丂丂丂丂係丏乣俇丂傕摨條偱偡丅
丂丂丂丂俈丏椺傪妛廗偡傞偲摨帪偵丄嫵壢彂俹俉丏偺椺俉偲栤俉丏傪妛廗偡傟偽姰惉偱偡丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂戞俆曬崘壽戣埲忋偱偡
丂戞俇曬崘壽戣
丂丂丂丂侾丏俀丏嫵壢彂俹俀俉嶲徠
丂丂丂仢俁師幃偺場悢暘夝偺岞幃
丂丂丂丂俁丏偼嫵壢彂俹俀俋嶲徠
丂丂丂仢俀師曽掱幃偺夝偒曽
丂丂丂丂係丏偼嫵壢彂俹係俉嶲徠偲摨帪偵儗億乕僩偺椺傪傛偔妛廗偟偰偔偩偝偄丅
丂丂丂丂丂丂丂乮係乯偺娭楢偲偟偰偨偲偊偽丄倃俀亅俆倃亖侽丂偼丂倃乮倃亅俆乯亖侽偐傜倃亖
侽丆倃亖俆偲側傝傑偡偺偱丄拲堄偱偡丅
丂丂丂丂俆丏偼嫵壢彂俹俁俀偵暯曽崻偺暅廗偑偁傝傑偡
丂丂丂丂俇丏俈偼儗億乕僩偺椺傪傛偔妛廗偟偨偆偊偱嫵壢彂俹俁俁傪嶲徠偟偰傗偭偰傒偰偔偩偝偄丅
丂丂丂丂丂丂俈丏偺椺偺側偐偱乮
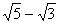 乮
乮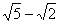 乯
亖丒丒丒丒偲偁傝傑偡偑丄乮
乯
亖丒丒丒丒偲偁傝傑偡偑丄乮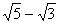 乯偼乮
乯偼乮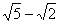 乯偺岆傝偱偡丅掶惓偟偰偍偄偰偔偩偝偄丅
乯偺岆傝偱偡丅掶惓偟偰偍偄偰偔偩偝偄丅
丂丂丂丂俉丏偼桳棟壔偺栤戣偱偡丅儗億乕僩偺椺侾丏椺俀傪妛廗偡傞偲偲傕偵嫵壢彂俹俁係丏偺椺俇丏椺戣侾傕妛廗偺偆偊偲傝偐偐偭偰偔偩偝偄丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂戞俇曬崘壽戣埲忋偱偡
丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂寬摤傪婩傝傑偡
(2008.9.25)